小學數學六年級幾何專題匯總

1、(★★)如圖，已知四邊形ABCD中，AB=13，BC=3，CD=4，DA=12，并且BD與AD垂直，則四邊形的面積等于多少?

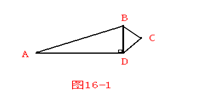
[思 路]：顯然四邊形ABCD的面積將由三角形ABD與三角形BCD的面積求和得到.三角形ABD是直角三角形，底AD已知，高BD是未知的，但可以通過勾股定理求出，進而可以判定三角形BCD的形狀，然后求其面積.這樣看來，BD的長度是求解本題的關鍵.

解：由于BD垂直于AD，所以三角形ABD是直角三角形.而AB=13，DA=12，由勾股定理，BD =AB -AD =13 —12 =25=5 ，所以BD=5.三角形BCD中BD=5，BC=3，CD=4，又3 十4 =5 ，故三角形BCD是以BD為斜邊的直角三角形，BC與CD垂直.那么：

= + =12×5÷2+4×3÷2=36..

即四邊形ABCD的面積是36.

2、(★★)如圖四邊形土地的總面積是48平方米，三條線把它分成了4個小三角形，其中2個小三角形的面積分別是7平方米和9平方米.那么最大的一個三角形的面積是________平方米;

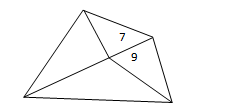
[分析]:剩下兩個三角形的面積和是 48-7-9=32 ，是右側兩個三角形面積和的2 倍，故左側三角形面積是右側對應三角形面積的2倍，最大三角形面積是 9×2=18。

3.(★★)將下圖中的三角形紙片沿虛線折疊得到右圖，其中的粗實線圖形面積與原三角形面積之比為2:3。已知右圖中3個陰影的三角形面積之和為1，那么重疊部分的面積為多少? 

[思 路]：小升初中常把分數，百分數，比例問題處理成份數問題，這個思想一定要養成。

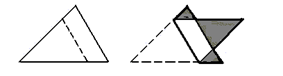
解：粗線面積：黃面積=2：3

綠色面積是折疊后的重疊部分，減少的部分就是因為重疊才變少的，這樣可以設總共3份，后來粗線變2份，減少的綠色部分為1份，所以陰影部分為2-1=1份，

4、(★★)求下圖中陰影部分的面積：

【解】如左下圖所示，將左下角的陰影部分分為兩部分，然后按照右下圖所示，將這兩部分分別拼補在陰影位置。可以看出，原題圖的陰影部分等于右下圖中AB弧所形成的弓形，其面積等于扇形OAB與三角形OAB的面積之差。

所以陰影面積：π×4×4÷4-4×4÷2=4.56。

5、(★★)下圖中陰影部分的面積是多少厘米2?

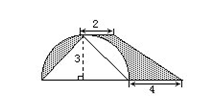
分析與解：本題可以采用一般方法，也就是分別計算兩塊陰影部分面積，再加起來，但不如整體考慮好。我們可以運用翻折的方法，將左上角一塊陰影部分(弓形)翻折到半圓的右上角(以下圖中虛線為折痕)，把兩塊陰影部分合在一起，組成一個梯形(如下圖所示)，這樣計算就很容易。

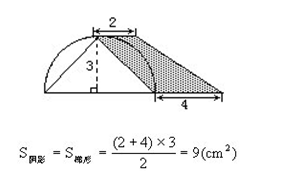
本題也可看做將左上角的弓形繞圓心旋轉90°，到達右上角，得到同樣的一個梯形。

如需下載完整版可以掃描下方二維碼即可免費獲取小學數學六年級幾何專題匯總電子版↓↓↓