2021年冀教版五年級上冊第六單元多邊形的面積試題解析

例1：小紅家一個長方形晾衣架不小心被她弄扁了，比原來矮了5厘米，你知道這個晾衣架的面積有什么變化嗎?變化了多少?

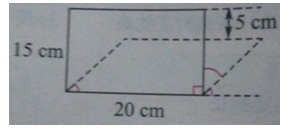
解析：此題考查了平行四邊形的面積。根據題意可知晾衣架由原來的長方形變成了平行四邊形。長方形的面積=長×寬，平行四邊形的面積=底×高，由圖可知長方形的長等于平行四邊形的底，平行四邊形的高，比原來長方形的寬變小了5厘米。所以平行四邊形的面積比原來長方形的面積變小了。然后根據長方形、平行四邊形的面積公式求出各自的面積，進行比較即可。

答案：長方形的面積：20×15=300(平方厘米)

平行四邊形的面積：20×(15-5)=200(平方厘米)

300-200=100(平方厘米)

答：這個晾衣架的面積比原來減少了，減少了100平方厘米。

例2：一個平行四邊形的面積是42平方分米，與它等底等高的三角形的底是3分米，高是多少?

解析：此題考查了平行四邊形是與它等底等高的三角形面積的2倍。解題關鍵知道題意中三角形和平行四邊形等底等高。根據題意因為三角形和平行四邊形等底等高，所以用平行四邊形的面積÷底=高，即42÷3=14(分米)。

答案：42÷3=14(分米)

答：三角形的高是14分米。

例3：求出三角形斜邊上的高。

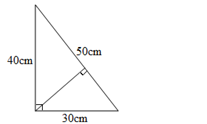
解析：此題考察了三角形的面積。解題關鍵直角三角形的面積等于兩條直角邊的積÷2，也等于斜邊乘以斜邊上的高÷2。即40×30÷50=24(厘米)。

答案： 40×30÷50=24(厘米)

答：斜邊上的高是24厘米。

例4：計算下面梯形的面積。(單位：厘米)

解析：此題考查了梯形面積的靈活運用。解題關鍵從圖中可以看出梯形的上底所在的三角形是一個等腰直角三角形，梯形的下底所在的三角形也是一個等腰直角三角形，并且上底與下底的和等于高。根據梯形的面積公式可得18×18÷2=162(平方厘米)

答案：18×18÷2=162(平方厘米)

例5：如圖：兩個完全一樣的三角形重疊在一起，求陰影部分的面積。單位：厘米。

解析：由圖意可知陰影部分的面積=三角形DEF的面積—三角形GEC的面積;梯形ABEG的面積=三角形ABC的面積—三角形GEC的面積;三角形ABC的面積=三角形DEF的面積;因此梯形的面積ABEG的面積=陰影部分的面積。

答案：(7-3+7)×3÷2

=11×3÷2

=16.5(平方厘米)

答：陰影部分的面積 是16.5平方厘米。

如需下載完整版可以掃描下方二維碼即可免費獲取2021年冀教版五年級上冊第六單元多邊形的面積試題解析電子版↓↓↓