2021年北師大版五年級上冊第六單元組合圖形的面積試題解析

【例1】向陽小學要油漆20扇教室門的外面(如圖)。

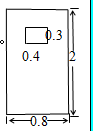
那么需要油漆的面積是多少平方米?

解析：要求油漆20扇教室的門的外面需要油漆的面積，要先

求出一扇門的外面需要油漆的面積，我們可以運用分割法將圖中的一扇門，分割成兩部分，一部分是們的整體，長為2米，寬為0.8米的一個大長方形;另一部分是門上的小窗，長為0.4米，寬為0.3米的小長方形，用大長方形的面積減去小長方形的面積即可得到油漆一扇門的外面需要油漆的面積。再用油漆一扇門的面積乘20扇門便可得到一共需要油漆的面積。

解答：(2×0.8-0.3×0.4)×20=29.6平方米

【例2】用不同的方法計算下面圖形的面積：

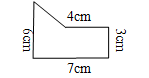
方法一：分析：首先運用分割法將組合圖形分為一個梯形和一個長方形，它的面積是就是梯形和長方形的面積和(如下圖)。

解答：3×4+(3+6)×(7-4)÷2=12+9×3÷2=12+27÷2=12+13.5=25.5(cm2)

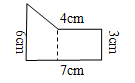
方法二：分析：

利用添補法補上一個梯形，使它成為一個大的長方形，原組合圖形的面積就是長方形的面積減去梯形的面積(如下圖)

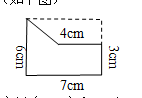
解答：6×7-(4+7)×(6-3)÷2=42-11×3÷2=42-33÷2=42-16.5=25.5(cm2)

【例3】

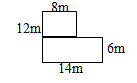
計算下面組合圖形的面積

解析：此題可以運用割補法將不規則圖形的上部割下來，補在圖形的右側或左側，這樣得到的長方形的面積就是原圖形的面積(如下圖)。

解答：(14+8)×6=132(m2)

【例4】開墾一塊邊長是200米的正方形荒地，這塊荒地的面積是多少公頃?

解析：正方形荒地的邊長是200米，正方形的面積=邊長×邊長，即200×200=40000(平方米)，根據1公頃=10000平方米，可知40000平方米=4公頃。

解答：200×200=40000(平方米) 40000平方米=4公頃

答：這塊荒地的面積是4公頃。

要點提示：

把陰影部分圖形的面積轉化成等底等高的三角形的面積來解答是關鍵。

【例5】在四邊形ABCD中，M為AB的中點，N為CD的中點，如果四邊形ABCD的面積是80cm2，求陰影部分BNDM的面積。

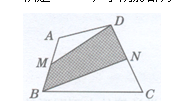
分析： 圖中陰影部分BNDM是一個不規則的四邊形，不能直接求出它的面積，可以用一條對角線BD將四邊形ABCD分成兩個三角形，如下圖所示。在三角形ABD和三角形BDC中，由于M、N分別是AB、CD的中點，根據等底等高的三角形面積相等可知：三角形AMD的面積等于三角形MBD的面積，三角形DNB的面積等于三角形CNB的面積。所以陰影部分的面積與空白部分的兩個三角形的面積之和相等，都是整個圖形面積的一半。

解答： 80÷2=40(cm2)

答：陰影部分BNDM的面積是40cm2。

如需下載完整版可以掃描下方二維碼即可免費獲取2021年北師大版五年級上冊第六單元組合圖形的面積試題解析電子版↓↓↓