2021年西師大版五年級上冊第四單元小數混合運算試題解析

第四單元 小數混合運算

【例1】甲乙二人分別從相距3.6千米的A、B兩地相向而行，甲每分鐘行0.05千米，乙每分鐘0.07千米，甲乙二人經過多長時間會相遇?

要點提示：

總路程÷相對速度=相遇時間。

思路分析：根據題意可知，甲行的路程加上乙行的路程就是AB兩地間的距離。甲乙二人每同時行走1分鐘，他們之間的距離就減少(0.05+0.07)千米，要想知道甲乙二人經過多少時間相遇，就要看AB間的距離中有多少個(0.05+0.07)千米，有幾個就說明經過了幾分鐘才相遇。

解答： 3.6÷(0.05+0.07)

=3.6÷0.12

=30(分鐘)

答：甲乙二人經過30分鐘會相遇。

【例2】用簡便算法計算：7.2×0.25+0.8×0.75。

要點提示：

有些表面上不符合運算的算式，可以通過等價變形轉化成符合運算定律的形式，再簡便運算。

思路分析：通過觀察，發現7.2和0.8、0.25與0.75都有很明顯的倍比關系，根據因數與積之間的關系，可以將7.2×0.25變成2.4×3×0.25=2.4×0.75，0.8×0.75變成0.8×3×0.25=2.4×0.25，然后根據乘法分配律進行計算;也可以將0.8×0.75變成0.8×3×0.25=2.4×0.25，7.2×0.25不變，然后根據乘法分配律進行計算。

解答：方法一 方法二

7.2×0.25+0.8×0.75 7.2×0.25+0.8×0.75

=2.4×0.75+2.4×0.25 =7.2×0.25+2.4×0.25

=2.4×(0.75+0.25) =0.25×(7.2+2.4)

=2.4×1 =0.25×9.6

=2.4 =2.4

【例3】有一項修水渠的工程,工程總長是18.5千米。第一期工程計劃修7.5千米,18天能完成,由于采用了先進設備,結果提前3天完成。照這樣的速度,剩下的工程多少天能完成?

思路分析：從問題出發,去尋求解決問題所必需的兩個條件,即實際每天的工作量和剩余的工作量。這兩個條件題目中都沒有直接給出,需要把這兩個所必需的未知條件作為問題,再去尋找解決它們所必需的條件。

分析如下圖:

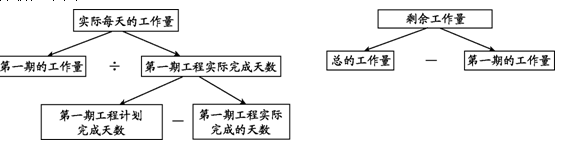
要點提示：

由問題出發去尋找解決問題的條件是關鍵。

解答： (18.5-7.5)÷[7.5÷(18-3)]

=11÷[7.5÷15]

=11÷0.5

=22(天)

答:剩下的工程22天能完成。

如需下載完整版可以掃描下方二維碼即可免費獲取2021年西師大版五年級上冊第四單元小數混合運算試題解析電子版↓↓↓