2021年西師大版六年級上冊第二單元圓試題解析

【例1】在下面的正方形中畫一個最大的圓。

思路分析：通過之前的學習，我們知道，對于一個圓來說，其圓心確定圓的位置，半徑決定圓的大小。要在這個正方形中畫一個最大的圓，那這個圓的圓心就應該是正方形的中心(兩條對角線的交點)，圓的直徑應該等于這個正方形的邊長。

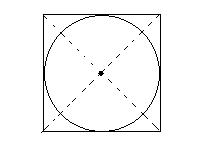
解答：先畫出正方形的兩條對角線，然后以對角線的交點為圓心，正方形邊長的一半為半徑畫圓，所得的圓就是最大的圓。如下圖：

要點提示：

正方形的中心是正方形兩條對角線的交點,也是最大圓的圓心。

【例2】如右圖，已知長方形的長是36厘米，則圓的半徑和直徑分別是多少厘米?

思路分析：從圖中可以看出，長方形中間的完整的圓和兩邊的兩個半圓的直徑是相等的，都等于長方形的寬。另外，兩邊的半圓的半徑加上中間大圓的直徑剛好等于長方形的長，所以長方形的長正好等于它們的半徑的4倍，即用長方形的長除以4就可以求出它們的半徑，再根據半徑與直徑的關系求出直徑。

要點提示：

長方形的長正好等于圓的半徑的4倍。

解答：24÷4=6(厘米) 6×2=12(厘米)

答：圓的半徑和直徑分別是6厘米、12厘米。

【例3】用兩種方法把四個直徑是16厘米的圓柱形木料捆扎在一起,截面如下圖所示。求這兩種方法分別需要多少厘米的繩子。

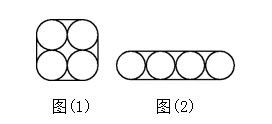
思路分析：圖(1)：在一個圓周上環繞的繩子長度是這個圓的周長的 ,四個角上共四個圓周，正好是一個圓的周長,即3.14×16=50.24(厘米)。四邊兩圓之間水平的線段,每條線段的長度正好等于兩個圓的半徑的和,也就是直徑的長度,有4條線段,即水平線段的長度為4×16=64(厘米)。

圖(2)：在一個圓周上環繞的繩子長度是這個圓的周長的 ,兩邊的兩個圓周加起來正好是一個圓的周長,即3.14×16=50.24(厘米)。上面或下面相鄰兩個圓之間水平的線段,每條線段正好等于三個圓的直徑的和,兩條線段就是六個圓的直徑的和,即6×16=96(厘米)。

解答：3.14×16+4×16=50.24+64=114.24(厘米)

3.14×16+6×16=50.24+96=146.24(厘米)

答:圖(1)方法用去了114.24厘米的繩子,圖(2)方法用去了146.24厘米的繩子。

如需下載完整版可以掃描下方二維碼即可免費獲取2021年西師大版六年級上冊第二單元圓試題解析電子版↓↓↓