2021年人教版五年級上冊第七單元數(shù)學廣角—植樹問題試題解析

第七單元 數(shù)學廣角—植樹問題

【例1】如下圖，每兩塊正方形瓷磚中間貼一塊長方形彩磚。像這樣一共貼了50塊長方形彩磚，那么正方形瓷磚有( )塊(第一塊和最后一塊都是正方形瓷磚)。

解析：本題考查的知識點是利用植樹問題的模型思想解答鋪磚問題。觀察圖中共有9塊長方形彩磚，10塊正方形瓷磚。由于第一塊和最后一塊都是正方形瓷磚，所以正方形瓷磚比長方形彩磚多1塊，長方形彩磚有50塊，那么正方形瓷磚就有51塊。

解答：51

【例2】把10根橡皮筋連接成一個圈，需要打( )個結(jié)。

解析：本題考查的知識點是在封閉曲線上的植樹問題(間隔數(shù)=植樹棵數(shù))。解答時，首先明確這道題是在封閉曲線上的植樹問題，有10根橡皮筋相當于間隔數(shù)是10，打結(jié)的個數(shù)就相當于植樹棵數(shù)。因為在封閉曲線上間隔數(shù)=植樹棵數(shù)，所以打結(jié)的個數(shù)是10。

解答：10。

【例3】丫丫和玲玲同住一幢樓，每層樓之間有20 級臺階，丫丫住二樓，玲玲住五樓。丫丫要從自己家到玲玲家去找她玩，需要走( )級臺階。

解析：本題考查的知識點是植樹問題數(shù)學模型的逆向應用。解答時，先明確每層樓之間有20級臺階，相當于間隔是20。從二樓到五樓有3個間隔，求需要走多少級臺階也就是求總數(shù)，所以用20×3，得到答案為60。

解答：60

【例4】小東把一些5角的硬幣平均排列在一張正方形紙的周邊，每邊的硬幣數(shù)相等，這些硬幣的總面值是12元。每邊最多能放( )枚硬幣。

解析：本題考查的知識點是用封閉曲線上的植樹問題模型綜合解決問題。解答時，先用12÷0.5=24求出一共有24枚硬幣。根據(jù)在封閉曲線上的植樹問題模型，正方形四周有24枚硬幣就有24個間隔，24÷4=6，每條邊有6個間隔。要使每邊硬幣數(shù)量最多，就要兩端都放。在兩端都栽的植樹問題中，植樹棵數(shù)=間隔數(shù)+1，因此每邊最多能放6+1=7枚硬幣。

解答：7

【例5】西苑小區(qū)車位不足，在小區(qū)路的一邊每5 m安置一個車位，用“⊥”標志隔開，在一段100 m長的路邊最多可停放多少輛車?需要畫多少個“⊥”標志?

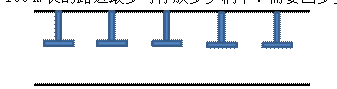
解析：本題考查的知識點是利用兩端不植樹問題的模型來解答小區(qū)停車位問題。

路的兩端不用畫“⊥”標志，相當于在一條線段上兩端都不栽的植樹問題。先用100÷5=20，求出有20個間隔，即可以停放20輛車;再用間隔數(shù)-1，求出植樹棵數(shù)， 20-1=19，也就是需要畫19個“⊥”標志。

解答：100÷5=20(輛) 20-1=19(個)

答：最多可停放20輛車，需要畫19個“⊥”標志。

如需下載完整版可以掃描下方二維碼即可免費獲取2021年人教版五年級上冊第七單元數(shù)學廣角—植樹問題試題解析電子版↓↓↓